2021-2025学年天津市和平区耀华中学八年级(上)期中数学试卷
网友分享
107340
试卷题目
1.下列交通安全图标不是轴对称图形的是( )(图中的三角形是等边三角形)
- A.

- B.

- C.

- D.

2.由下列长度组成的各组线段中,不能组成三角形的是( )
- A. 1cm,3cm,3cm
- B. 2cm,5cm,6cm
- C. 8cm,6cm,4cm
- D. 14cm,7cm,7cm
3.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
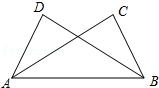

- A. AC=BD
- B. ∠CAB=∠DBA
- C. ∠C=∠D
- D. BC=AD
4.一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
- A. 五边形
- B. 六边形
- C. 七边形
- D. 八边形
5.已知点P(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是( )
- A. a<-1
- B. -1<a<
3 2 - C. -<a<1
3 2 - D. a>
3 2
6.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,则判定△ADC与△AEB全等的依据是( )
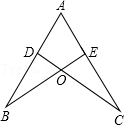

- A. SSS
- B. SAS
- C. ASA
- D. AAS
7.如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
①AB=AC=CE;②AB+BD=DE;③AD=
AE;④BD=DC=CE.
其中,正确的结论是( )
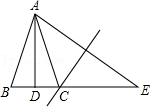
①AB=AC=CE;②AB+BD=DE;③AD=
| 1 |
| 2 |
其中,正确的结论是( )

- A. 只有①
- B. 只有①②
- C. 只有①②③
- D. 只有①④
8.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( )
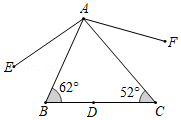

- A. 126°
- B. 128°
- C. 130°
- D. 132°
9.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
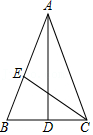

- A. 20°
- B. 35°
- C. 40°
- D. 70°
10.如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的有( )
①△BDF,△CEF都是等腰三角形;②DE=DB+CE;③△ADE的周长等于AB+AC;④BF=CF.
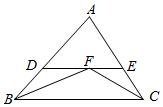
①△BDF,△CEF都是等腰三角形;②DE=DB+CE;③△ADE的周长等于AB+AC;④BF=CF.

- A. 1个
- B. 2个
- C. 3个
- D. 4个
11.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
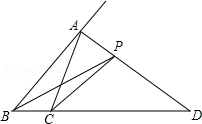

- A. m+n>b+c
- B. m+n<b+c
- C. m+n=b+c
- D. 无法确定
12.已知:如图,△ABC中,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )

















