2021-2025学年山东省聊城市东昌府区八年级(上)期中数学试卷
网友分享
107316
试卷题目
1.下列图形中,轴对称图形的是( )
- A.

- B.

- C.

- D.

2.在式子
,
,
,
,
+
,
中,分式的个数是( )
| 1 |
| a |
| 2xy |
| π |
| 3a2b3c |
| 4 |
| 5 |
| 5+x |
| x |
| 7 |
| y |
| 8 |
| x2 |
| x |
- A. 2
- B. 3
- C. 4
- D. 5
3.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第几块去,这利用了三角形全等中的什么原理( )
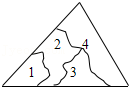

- A. 2;SAS
- B. 4;ASA
- C. 2;AAS
- D. 4;SAS
4.下列各式从左到右的变形正确的是( )
- A. =
x- y1 2 x+y1 2 2x-y x+2y - B. =
0.2a+b a+0.2b 2a+b a+2b - C. =
x+1 x-y x-1 x-y - D. =
a+b a-b a-b a+b
5.若把分式
中的x和y都扩大2倍,那么分式的值( )
| x+y |
| xy |
- A. 扩大2倍
- B. 不变
- C. 缩小为原来的
1 2 - D. 缩小为原来的
1 4
6.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
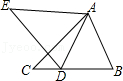

- A. 6cm
- B. 5cm
- C. 7cm
- D. 无法确定
7.若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是( )
- A. -5
- B. -3
- C. 3
- D. 1
8.如图,△ABC中,AB=7cm,BC=5cm,AC=6cm,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长为( )
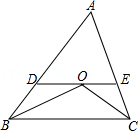

- A. 13cm
- B. 14cm
- C. 15cm
- D. 16cm
9.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
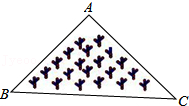

- A. △ABC的三条中线的交点
- B. △ABC三条角平分线的交点
- C. △ABC三条高所在直线的交点
- D. △ABC三边的中垂线的交点
10.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果P也是图中的格点,且使得△ABP为等腰三角形,则点P的个数是( )
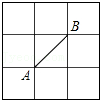

- A. 5
- B. 6
- C. 7
- D. 8
11.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于
MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=5,AB=18,则△ABD的面积是( )
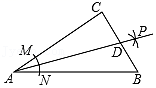
| 1 |
| 2 |

- A. 15
- B. 30
- C. 45
- D. 60
12.如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F,若S△ABC=7,DE=2,AB=4,则AC的长为( )
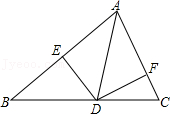

- A. 3
- B. 4
- C. 5
- D. 6
13.如果分式
的值为0,那么x的值为 .
| |x|-1 |
| x+1 |
14.各分式
,
,
的最简公分母是 .
| 1 |
| x2-1 |
| x-1 |
| x2-x |
| 1 |
| x2+2x+1 |
15.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB= 度.
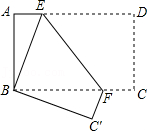

16.已知点P到x轴,y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是 .
17.观察下面一列分式:
,
,
,
,
,…根据你的发现,第n项是 .
| 1 |
| x |
| 2 |
| x2 |
| 4 |
| x3 |
| 8 |
| x4 |
| 16 |
| x5 |
18.化简:
(1)
⋅
.
(2)
÷
.
(3)(
)2÷
×(
).
(4)
×
÷
.
(1)
| x2+x |
| x |
| 2x |
| x+1 |
(2)
| x+3 |
| x2-2x+1 |
| x2+3x |
| (x-1)2 |
(3)(
| ab |
| 2c |
| -3ab |
| 4cd |
| -3 |
| 2d |
(4)
| a+2 |
| a2-2a+1 |
| a2-4a+4 |
| a+1 |
| a2-4 |
| a2-1 |
19.已知:|x-4|+(y−9)2=0,试求代数式:(
)2×
÷(
)2的值.
| y-x |
| y+x |
| x+y |
| x2-4xy+4y2 |
| x-y |
| x-2y |
20.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,1)、B(4,2)、C(3,4).
(1)若△A1B1C1与△ABC关于y轴成轴对称,请在图中作出△A1B1C1,并写出△A1B1C1三个顶点A1,B1,C1的坐标;
(2)若点P为x轴上一点,在图中画出点P,使PA+PB的值最小,则点P的坐标为 ;
(3)计算△ABC的面积.
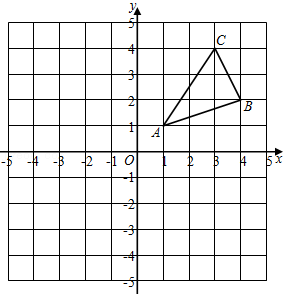
(1)若△A1B1C1与△ABC关于y轴成轴对称,请在图中作出△A1B1C1,并写出△A1B1C1三个顶点A1,B1,C1的坐标;
(2)若点P为x轴上一点,在图中画出点P,使PA+PB的值最小,则点P的坐标为 ;
(3)计算△ABC的面积.

21.如图,已知AD平分∠BAC交BC于D,DE⊥AB,DF⊥AC,垂足分别是E、F,求证:AD垂直平分EF.









